| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Google Excel
- list
- Tkinter
- Google Spreadsheet
- SQL
- hive
- array
- django
- 파이썬
- Python
- matplotlib
- math
- Redshift
- c#
- GIT
- PANDAS
- PostgreSQL
- numpy
- Presto
- gas
- google apps script
- dataframe
- Kotlin
- string
- Java
- Github
- PySpark
- Apache
- Excel
- Today
- Total
달나라 노트
Python numpy : random normal, random uniform (정규 분포, 균등 분포, 정규 분포 array, 균등 분포 array, normal distribution, uniform distribution) 본문
Python numpy : random normal, random uniform (정규 분포, 균등 분포, 정규 분포 array, 균등 분포 array, normal distribution, uniform distribution)
CosmosProject 2022. 1. 23. 01:12
numpy의 normal method는 특정 구간 사이의 값을 정규분포의 형태로 추출해줍니다.
numpy의 uniform method는 특정 구간 사이의 값을 균등분포의 형태로 추출해줍니다.
이게 무슨 소린지 지금은 잘 감이 안올겁니다.
실제 예시를 보시죠.
먼저 normal method (정규분포)를 봅시다.
import numpy as np
arr_normal_distribution = np.random.normal(loc=0, scale=10, size=10000)
print(arr_normal_distribution)
-- Result
[ 6.95222556 -5.13843794 1.64328595 ... -10.97587735 18.23262221
-21.6592955 ]normal method는 위처럼 사용할 수 있습니다.
첫 번째 인자인 loc는 정규분포 그래프의 평균(mean)을 의미합니다. 정규분포 그래프에서 가장 솟은 가운데 값을 의미하죠. (기본값은 0입니다. 왜냐면 표준정규분포의 평균이 0이기 때문이죠.)
두 번째 인자인 sacle은 정규분포 그래프의 표준편차(Standard deviation)를 의미합니다. (기본값은 1입니다. 왜냐면 표준정규분포의 표준편차가 1이기 때문이죠.)
세 번째 인자인 size는 추출할 숫자의 개수를 의미합니다.
즉, 위 예시의 의미는
모든 실수에 대해서 평균이 0, 표준편차가 10인 정규분포 그래프의 y값에 해당하는 확률을 부여하고 그 확률대로 총 10000개의 실수를 추출하라는 의미입니다.
이렇게 추출된 값들을 print해보니 사실 저 값만으로는 감이 오지 않습니다.
matplotlib의 hist method를 이용하여 histogram을 그려봅시다.
(matplotlib histogram 관련 내용 = https://cosmosproject.tistory.com/446)
import numpy as np
import matplotlib.pyplot as plt
arr_normal_distribution = np.random.normal(loc=0, scale=10, size=10000)
print(arr_normal_distribution)
plt.hist(arr_normal_distribution)
plt.title('normal distribution')
plt.show()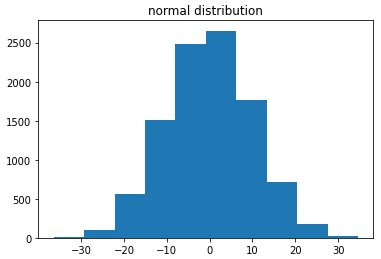
normal method로 추출된 값들을 기준으로 histogram을 그려봤는데 마치 정규분포 그래프와 비슷하게 나왔습니다.
이제 normal method가 어떻게 작동하는지 한번 정리해봅시다.
1. normal method는 parameter로서 평균값, 표준편차를 받으며 이걸 기준으로 대략적인 정규분포 그래프를 그립니다.
(실제로 그리는건 아닙니다만 저희가 이해하기 좋게 그린다고 받아들입시다.)
2. 그려놓은 정규분포 그래프의 x축은 우리에게 return해줄 숫자이며, y축은 x축에 있는 숫자가 추출될 확률을 의미합니다. 따라서 정규분포 그래프의 중간에 있는 숫자일수록 더 추출될 확률이 높습니다.
3. 결국 normal method에 전달된 중간값(loc 인자) 근처의 숫자는 더 많이 추출될 것이며, 중간값에서 멀어질수록 추출되는 개수가 적어질 것입니다.
4. 이렇게 추출된 값들의 histogram을 그려보면 위처럼 정규분포 그래프를 그립니다.
이걸 단순무식하게 한번 예를 들어보면
중간값을 0이라고 했을 때
-3 -> 1개
-2 -> 3개
-1 -> 8개
0 -> 15개
1 -> 8개
2 -> 3개
3 -> 1개
이처럼 0에 가까운 값들이 추출될 확률이 높으니 더 개수가 많으며,
0에서 멀어진 값일수록 추출되는 개수가 적습니다.
그러면 여기서 한가지 질문이 있습니다.
normal method에 의해 추출된 array에서 중복되는 값이 있을까요?
정답은 있을 수 있다 입니다.
normal method는 정규분포 그래프에 따라 y축을 확률로하여 숫자를 추출하기 때문에 중복된 값이 추출될 수도 있습니다.
-3 -> 1개
-2 -> 3개
-1 -> 8개
0 -> 15개
1 -> 8개
2 -> 3개
3 -> 1개
다만 실제로는 위 예시처럼 정수만 추출하지 않고 모든 실수들을 대상으로 추출하기 때문에 소수점까지 완전히 동일한 값이 추출되기는 어려울 뿐이죠.
이번에는 uniform method를 알아봅시다.
uniform method는 균등분포(uniform distribution) 그래프를 따른다고 했습니다.
uniform method를 이해하기 위해선 균등분포가 뭔지 먼저 알아야합니다.
정규분포와 비교를 해보겠습니다.
아래 정규분포 그래프를 봐봅시다.

매끄럽진 않지만 어쨌든 정규분포 그래프는 대략적으로 위와같은 모양을 가지고 있습니다.
누가봐도 정규분포 그래프는 x값에 따라 y값이 동일하지 않습니다.

위 그래프를 보면 x=0일때에는 y값이 거의 350정도 되는 것 같습니다.
하지만 x=20인 곳을 보면 y값은 약 50정도 되는걸 볼 수 있죠.
그래서 y축의 값이 x값이 뽑힐 확률이라고 했을 때 x가 0에 가까울수록 y값(확률)이 높기 때문에 normal method에 의해 더 많은 개수가 추출된겁니다.
이번에는 균등분포입니다.

위 균등분포 그래프를 보면 정규분포와는 달리 x값이 몇이건간에 y값이 거의 동일합니다.
균등분포의 의미는 x값이 몇인지 상관없이 y값이 동일한 그래프를 의미합니다.
그래서 y축을 x값이 뽑힐 확률이라고 했을 때 x값이 무엇이건 상관없이 y값(확률)이 동일하기 때문에 uniform method에 의해 추출될 확률도 동일합니다.
import numpy as np
arr_uniform_distribution = np.random.uniform(low=0, high=10, size=10000)
print(arr_uniform_distribution)
-- Result
[1.87548138 3.73175744 1.12371566 ... 8.69683621 9.92679663 2.94248609]uniform method는 위처럼 사용할 수 있습니다.
첫 번째 parameter인 low는 uniform method가 추출할 값의 최소치를 의미합니다.
두 번째 parameter인 high는 uniform method가 추출할 값의 최대치를 의미합니다.
세 번째 parameter인 size는 uniform method가 추출할 값의 개수를 의미합니다.
즉, 위 예시는 0 이상 10 미만 = [0, 10)인 구간에 존재하는 모든 실수에 동일한 확률을 부여하여 총 10000개의 실수를 추출하라는 의미입니다.
마찬가지로 uniform method로 만들어진 값이 각각 몇개씩 추출되었는지 가늠하기 위해 histogram을 그려보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
arr_uniform_distribution = np.random.uniform(low=0, high=10, size=100000)
print(arr_uniform_distribution)
plt.hist(arr_uniform_distribution, bins=10)
plt.title('uniform distribution')
plt.show()
uniform method로 인해 0 이상 10 미만인 구간에 존재하는 실수가 추출되었고 각각의 구간에 대해 추출된 실수의 개수는 거의 동일합니다.
이것이 균등분포(uniform distribution)입니다.
- 추가
균등분포에 대해 몇가지 예시를 들어보겠습니다.
보통 1부터 6까지라고 하면 두 가지로 나눠볼 수 있습니다.
1, 2, 3, 4, 5, 6의 정수 -> 불연속
1 이상 6 이하의 모든 실수 -> 연속
균등분포는 이 두가지 모두에 대해 적용할 수 있습니다.
주사위를 예로 들어보죠.
주사위는 1, 2, 3, 4, 5, 6의 숫자를 가지고 있습니다.
그리고 우리는 이미 주사위를 던졌을 때 이 각각의 숫자가 나올 확률이 동일하다는걸 알 수 있죠.
이것도 일종의 균등분포라고 할 수 있습니다.
1~6 구간의 정수에 대해 각각의 정수가 나올 확률이 동일하니까요.
다만 정수만 해당하기 때문에 불연속적이므로 불연속 균등 분포라고 합니다.
반면에 주사위가 아니라 1 이상 6 이하의 구간에 무한하게 존재하는 모든 실수를 상자에 넣어두고 하나씩 뽑는다고 가정한다면,
당연히 모든 실수가 뽑힐 확률은 동일합니다. 따라서 균등분포입니다.
다만 1 이상 6 이하의 구간에 무한하게 존재하는 모든 실수를 대상으로 하기 때문에 연속적이죠. 즉, 연속 균등 분포입니다.
자 다시 주사위로 돌아오죠.
주사위에서 1 이상 6 이하인 정수 각각이 뽑힐 확률은 얼마일까요?
간단하죠. 1/6입니다.
그러면 주사위에서 1 미만 또는 6 초과인 숫자가 뽑힐 확률은 얼마일까요?
마찬가지로 간단합니다. 0입니다.
주사위에서 0같은 숫자가 나올리가없죠.
이걸 그래프로 나타내보면 다음과 같습니다.

a에서 b의 구간에 대한 확률 f(x)는 모두 동일합니다.
a에서 b의 구간에 그려진 파란색 그래프를 보면 모두 동일한 y값을 가르키고있죠.
또한 a보다 작거나 b보다 큰 x 구간에 대해서는 y값이 0입니다.
또한 a에서 b의 구간에 있는 실수는 100%의 확률을 모두 동일하게 나눠가지므로 a에서 b 구간에 있는 모든 y값을 다 합치면 1(= 100%)이 된다는 의미입니다.
따라서 하늘색으로 칠해진 사각형의 면적을 구하면 그것은 1이 된다는 의미이겠죠.
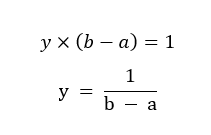
이 과정을 계산해보면 결국 위와 같습니다.
즉, y = f(x) = 1 / (b - a)가 되는 것이고 이것이 바로 균일분포의 확률밀도함수가 됩니다.
좀 더 자세히 나타내면 확률밀도함수는 아래와 같습니다.

a~b 구간을 벗어난 x값에 대해선 확률이 0이라는 부분까지 명시해주고있습니다.
'Python > Python numpy' 카테고리의 다른 글
| Python numpy : argmax, argmin (array에서 가장 큰 값의 index return, array에서 가장 작은 값의 index return) (0) | 2022.01.23 |
|---|---|
| Python numpy : split (array 나누기, array split) (0) | 2022.01.23 |
| Python numpy : random shuffle (array 랜덤하게 섞기) (0) | 2022.01.22 |
| Python numpy : random seed (예상되는 난수 생성하기) (0) | 2022.01.22 |
| Python numpy : sinh, cosh, tanh (0) | 2022.01.22 |

