| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- PySpark
- Google Spreadsheet
- Java
- Redshift
- google apps script
- GIT
- math
- Kotlin
- dataframe
- gas
- Github
- PANDAS
- hive
- 파이썬
- matplotlib
- string
- array
- numpy
- Python
- PostgreSQL
- list
- Google Excel
- Excel
- django
- SQL
- Mac
- Tkinter
- Apache
- c#
- Today
- Total
달나라 노트
백분위(Percentile Rank), 백분위수(Percentile), 사분위수(Quartile) 알아보기 본문
수학, 통계, 데이터 분석 등 다양한 곳에서 백분위라는 말이 쓰입니다.
수능 성적을 받아도 백분위라는 것이 있죠.
이 백분위라는 것이 무엇이고, 왜/어떻게 쓰이며, 어떻게 계산할 수 있는지 알아봅시다.
1. 백분위(Percentile Rank), 백분위수(Percentile)란?
한 세트의 여러 값들이 있을 때 각각의 값들이 이 세트 내에서 어느 정도의 위치에 존재하는지를 0% ~ 100%의 숫자로 표현하는 것을 백분위(Percentile Rank)라고 합니다.
보통 값들을 오름차순하여 정렬한 후
가장 작은 값은 0% 라는 백분위를
가장 큰 값은 100% 라는 백분위를 가지게 되며
그 사이의 값은 크면 클수록 더 100%에 가까운 값을 가지게 됩니다.
백분위수(Percentile)는 이렇게 계산된 한 세트의 값들 내에서 특정 위치(n%)에 있는 값을 백분위수라고 합니다.
백분위와 백분위수가 어떻게 사용되는지는 백분위, 백분위수에 대한 개념을 먼저 이해한 후 맨 아래에서 얘기하겠습니다.
2. 백분위 계산

위 이미지를 봅시다.
먼저 Value 컬럼은 현재 가지고 있는 값들의 세트입니다.
10, 20, 30, ..., 110의 총 11개의 값이 존재하며 이를 오름차순 해놨습니다.
오름차순을 한 이유는 백분위란 일반적으로 오름차순을 기준으로 숫자들의 위치를 계산하기 때문입니다.
Rank는 순위입니다.
=RANK(B3, $B$3:$B$13, 1)
사용된 수식은 위와 같으며, Value 컬럼의 값들의 순위를 오름차순으로 매긴 결과입니다.
즉, 가장 작은 값이 1위, 가장 큰 값이 11위를 가지게 되었죠.
Rank - 1 컬럼은 Rank 컬럼에서 1을 뺀 값입니다.
이렇게 하는 이유는 백분위를 계산할 때 백분위가 0% ~ 100%로 계산되어야 하기 때문에 1위가 0위로 표기되도록 바꾼 것입니다.
마지막 Percentile Rank 컬럼이 백분위를 계산한 결과를 나타내어줍니다.
=D3 / (COUNT($B$3:$B$13) - 1)
사용된 수식은 위와 같습니다.
이를 해석해 보면 다음과 같습니다.
Percentile Rank = (Rank - 1) / (Value Count - 1)
백분위는 각 값들에 해당하는 Rank - 1값을 값들의 총 개수 - 1 (Value Count - 1)로 나눈 것과 같습니다.
즉, Value = 30 값에 대한 Percentile Rank는
Value = 30에 대한 Rank = 3이므로 분모는 2 (= 3 - 1)
총 값의 개수가 11개 이므로 분자는 10 (= 11 - 1)
따라서 2 / 10 = 0.2가 Value = 30에 대한 백분위가 됩니다.
여기서 분모를 Value Count - 1로 하는 이유는
결국 백분위는 0% ~ 100% 범위의 숫자로 나타내어야 하고,
Rank - 1을 하여 가장 마지막 Rank가 모든 value 개수 - 1이 될 것이고,
따라서 Count에서도 1을 빼줘야 100%가 되기 때문입니다.
총 숫자의 개수는 11개인데 최대 Rank가 10이므로
총 수자의 개수 11에서 1을 빼지 않으면 가장 큰 숫자의 백분위가 10 / 11이라는 값으로 계산됩니다.
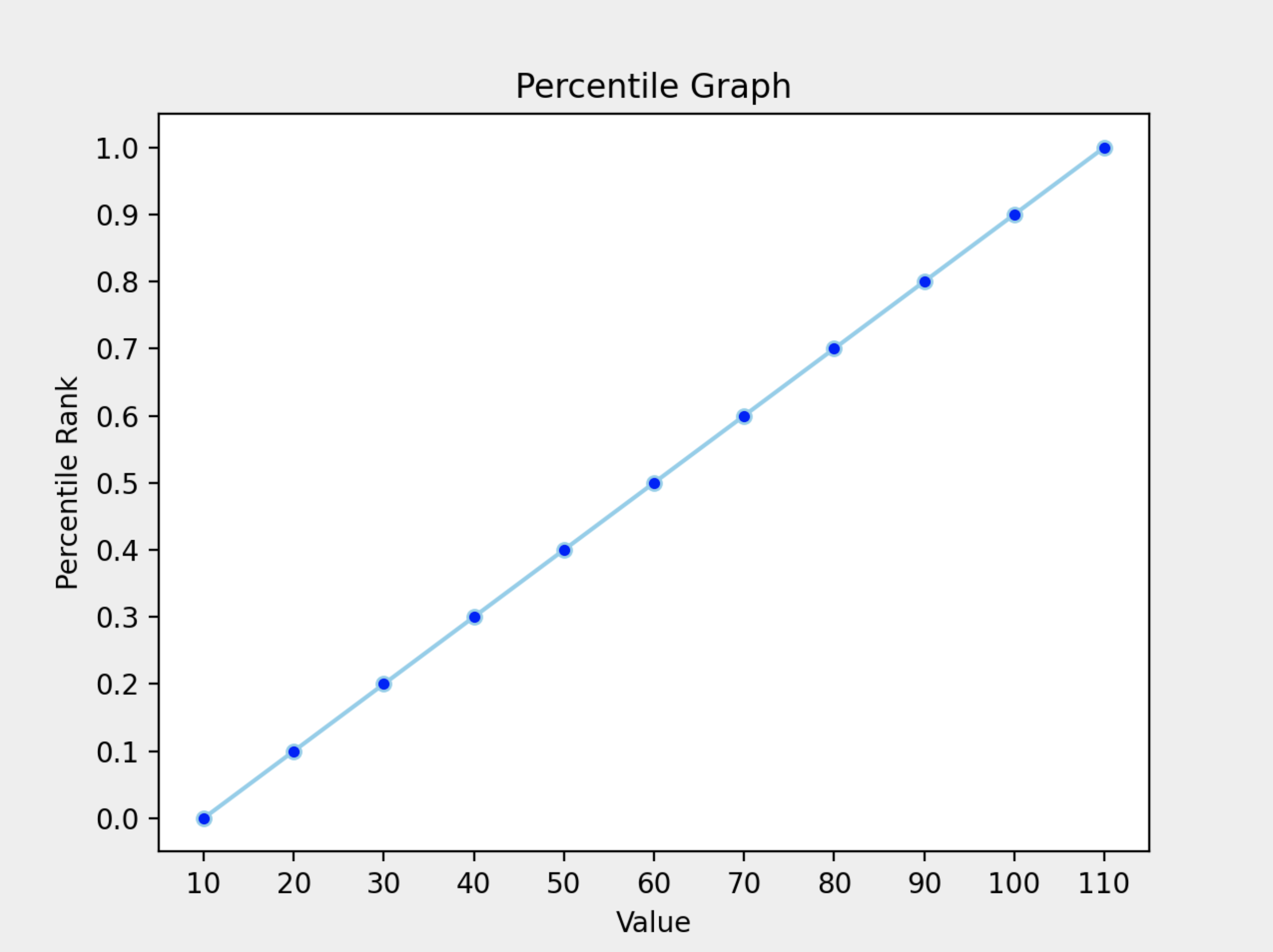
위에서 계산된 Value, Percentile의 값들을 그래프로 나타낸 예시입니다.
x축이 Value이고 y축이 각 값들에 대한 백분위를 나타냅니다.

위 이미지는 또 다른 백분위 계산의 예시입니다.
백분위는 값 중에서 음수가 있어도 되며 그 값들이 얼마나 크건 작건 상관 없습니다.
또한 값들의 크기가 어떠하건 백분위는 그냥 값들을 오름차순 했을 때 각각의 값들이 상대적으로 어느 정도의 위치에 속하는지를 나타내기 때문에 위처럼 값의 개수가 동일하다면 백분위의 종류 또한 동일합니다.
(절대 값이 압도적으로 크다고 해서 백분위가 커지지 않습니다. 백분위는 값들의 정비례 관계가 아닙니다.)
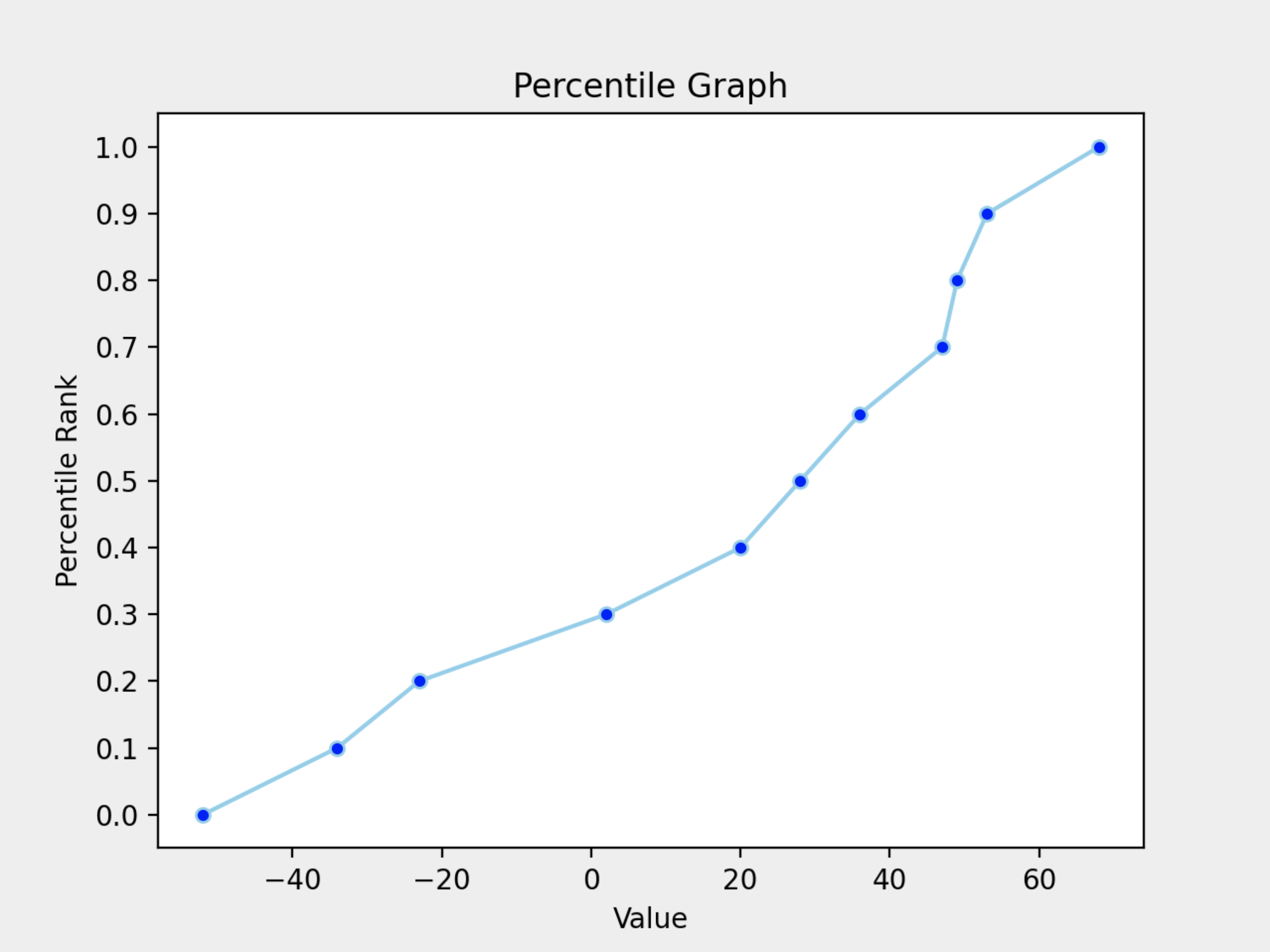
위에서 계산된 Value, Percentile의 값들을 그래프로 나타낸 예시입니다.
x축이 Value이고 y축이 각 값들에 대한 백분위를 나타냅니다.
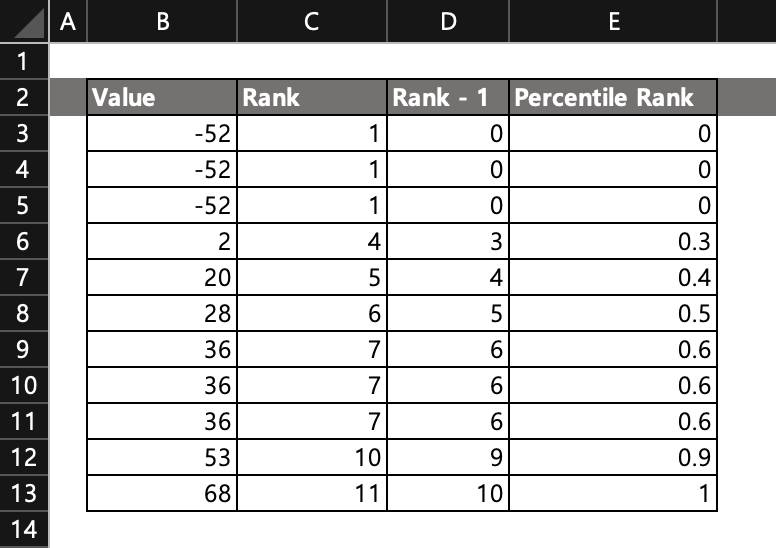
백분위는 위처럼 동일한 값이 존재해도 유효합니다.
위 예시를 보면 Rank = 1인 값이 3개가 존재하며
Rank = 7인 값도 3개가 존재합니다.
그래도 백분위는 동일하게 계산됩니다.
말한대로 값들 사이의 상대적인 위치이기 때문에 전혀 문제가 되지 않습니다.
3. 백분위수 계산
백분위수는 어떤 값들이 있을 때 이 값들 중에서 어떤 위치(n%)에 있는 값이 무엇일까 계산하는 것입니다.
처음에 봤던 예시를 다시 가져와보죠.

테이블이 2개가 되었습니다.
G column을 보면 백분위가 있고
H column을 보면 백분위수가 계산되어 있습니다.
=PERCENTILE.INC($B$3:$B$13, G3)
H3 cell에 쓰인 수식은 위와 같습니다.
(엑셀에서 PERCENTILE.INC()는 백분위수를 계산해주는 함수입니다.)
오른쪽 테이블을 보면 0.1에 대한 백분위수는 20으로 계산되어있죠.
이 말인 즉슨, Value 컬럼에 있는 11개의 값들이 있을 때
여기서 0.1 (= 10%) 위치에 있는 값이 무엇이냐 라는 것입니다.
왼쪽 테이블에서 이미 계산해둔 Percentile Rank를 보면 0.1(= 10%) 위치에 있는 값은 20이죠.
따라서 올바르게 계산된 것을 알 수 있습니다.
그러면 다음을 봅시다.
0.15 (= 15%)에 대한 백분위수도 계산할 수 있습니다.
오른쪽 테이블을 보면 0.15에 대한 백분위수는 25라고 나와있죠.
즉, Value 컬럼에 있는 11개의 값들을 기준으로 0% ~ 100%의 위치를 매겼을 때 15% 위치에 있는 값은 25라는 것입니다.
근데 Value를 기준으로 계산된 Percentile Rank를 보면 15%라는 위치는 존재하지 않습니다.
0, 0.1, 0.2, ..., 1 만 존재하죠.
그러면 어떻게 15% 위치의 백분위수를 계산한걸까요?
왼쪽 테이블에서
백분위 0.1에 대한 값은 10이고
백분위 0.2에 대한 값은 20입니다.
백분위 0.15는 백분위 0.1 ~ 백분위 0.2 사이에 있는 값입니다.
0.1로부터 0.05만큼 더해진 값이죠.
(또는 0.2로부터 0.05만큼 뺀 값이라고 볼 수도 있습니다.)
이렇게 백분위 0.1에 대한 값, 백분위 0.2에 대한 값을 알면 이 값들을 기준으로 가중치(weight)를 두어 백분위 0.15에 대한 백분위수를 구할 수 있습니다.
이 과정을 그래프로 나타내면 훨씬 더 보기 쉬워집니다.

파란색 선은 왼쪽 테이블에 있는 11개의 Value와 각 Value에 대한 백분위를 그래프로 나타낸 선입니다.
y축이 백분위이므로 y = 0.15일 때 x값은 몇일까를 생각해보면 25가 되죠.
(20, 0.1), (30, 0.2) 두 점을 잇는 직선의 방정식을 생각하면 편합니다.
이런 방식으로 0% ~ 100%에 있는 모든 백분위에 대한 값을 구할 수 있습니다.
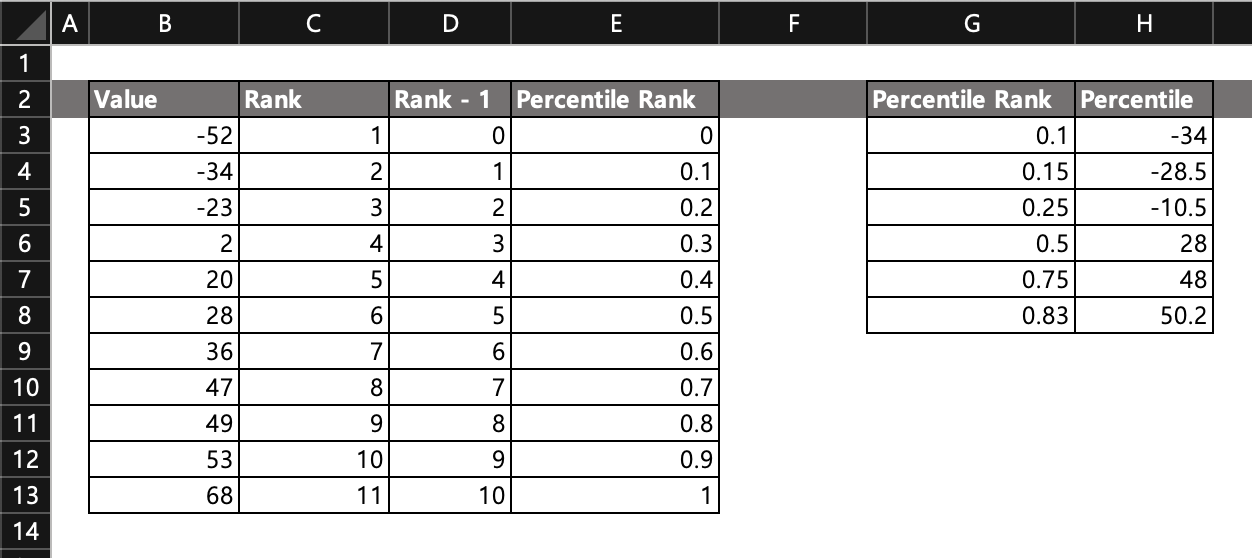
이번 예시도 Value의 종류만 다를 뿐 동일합니다.
오른쪽 테이블을 보면 다양한 백분위(Percentile Rank)에 대한 백분위수(Percentile)이 계산되어 있습니다.
백분위 0.1 (= 10%)에 대한 값은 -34입니다.
이것은 명확한게 왼쪽 테이블을 보면 이미 백분위 0.1에 대한 값이 -34라는 것을 알 수 있습니다.
문제는 백분위 0.15(= 15%)에 대한 값이죠.
구하는 원리는 이전에 봤던 것과 똑같습니다.
0.15는 왼쪽 테이블에서 현재 알고있는 값들에 대한 백분위 0.1 ~ 0.2 사이에 있는 값입니다.
값 -34에 대한 백분위는 0.1이고
값 -23에 대한 백분위는 0.2입니다.
따라서 이 두 점 사이의 기울기를 구해서 백분위를 구할 수 있다는 것이죠.
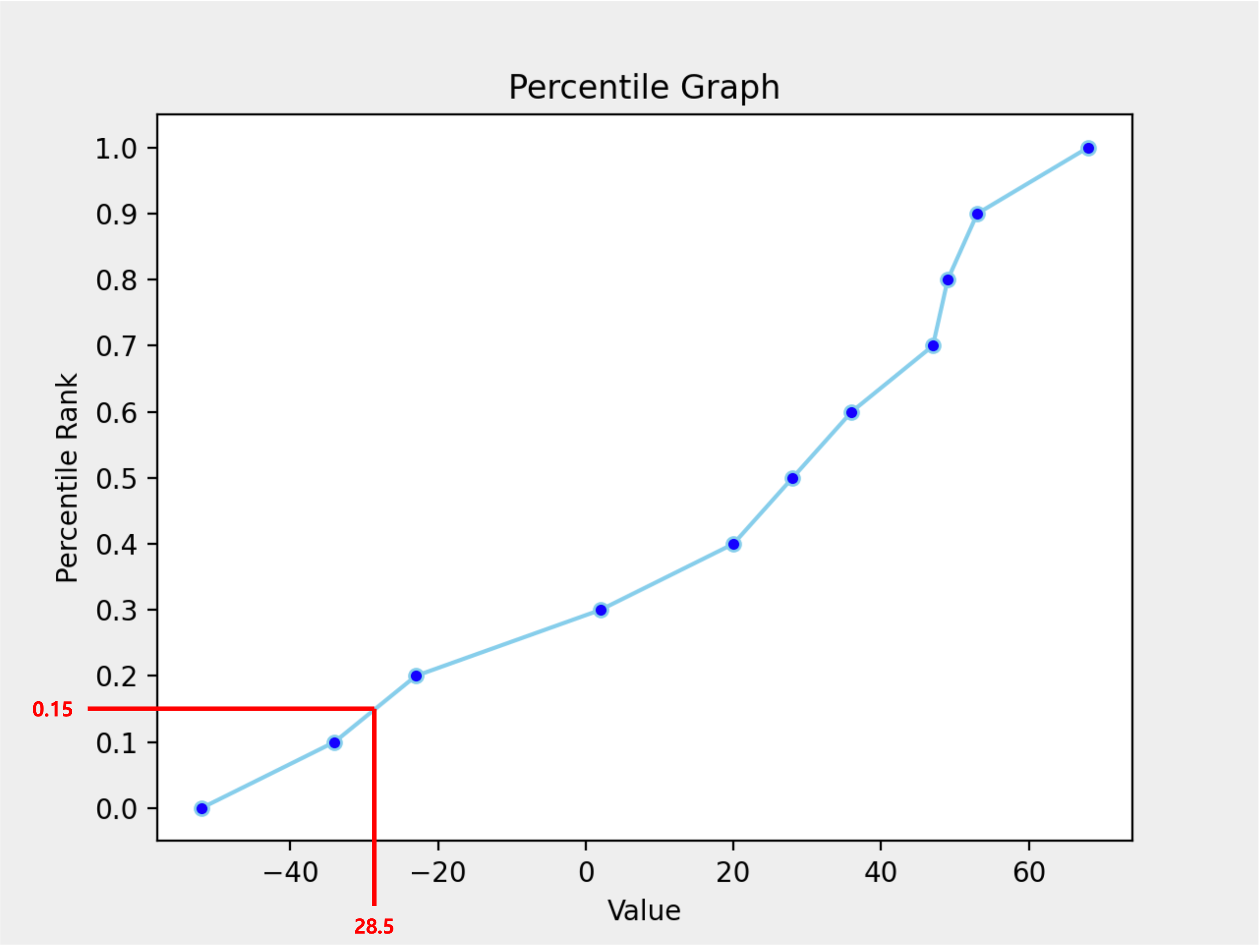
그래프로 나타내면 위와 같습니다.
간단하죠?
한 가지 주의할 점은 이번 예시에선 주어진 Value들 간의 간격이 일정하지가 않다는 것입니다.
따라서 각 백분위 사이의 그래프의 기울기도 Value의 구간마다 다 다릅니다.
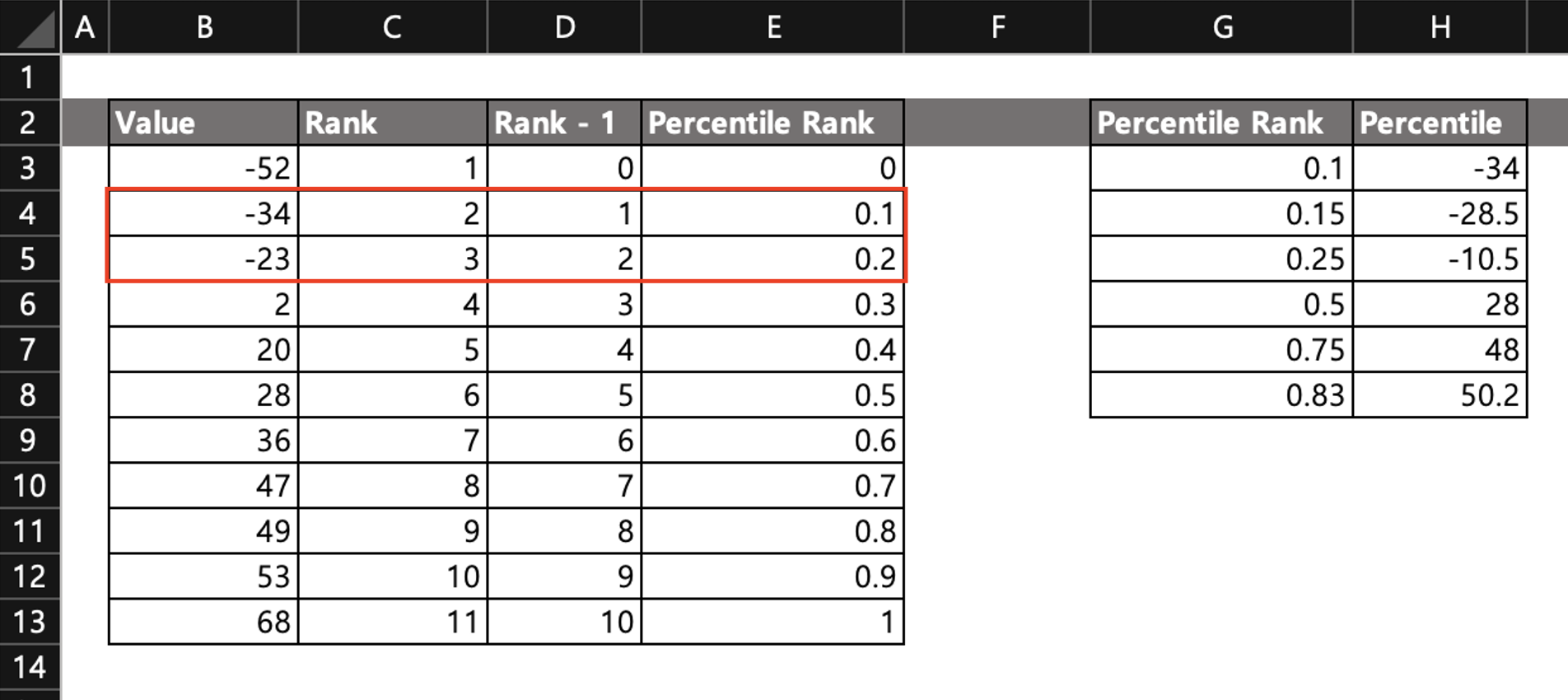
위 이미지에서 처럼 Value에 있는 값들을 기준으로 백분위를 구했을 때
백분위 0.15에 가장 근접한 백분위는 0.1과 0.2입니다.
따라서 0.1 ~ 0.2 백분위 사이의 기울기를 기준으로 백분위 값을 구해야 합니다.
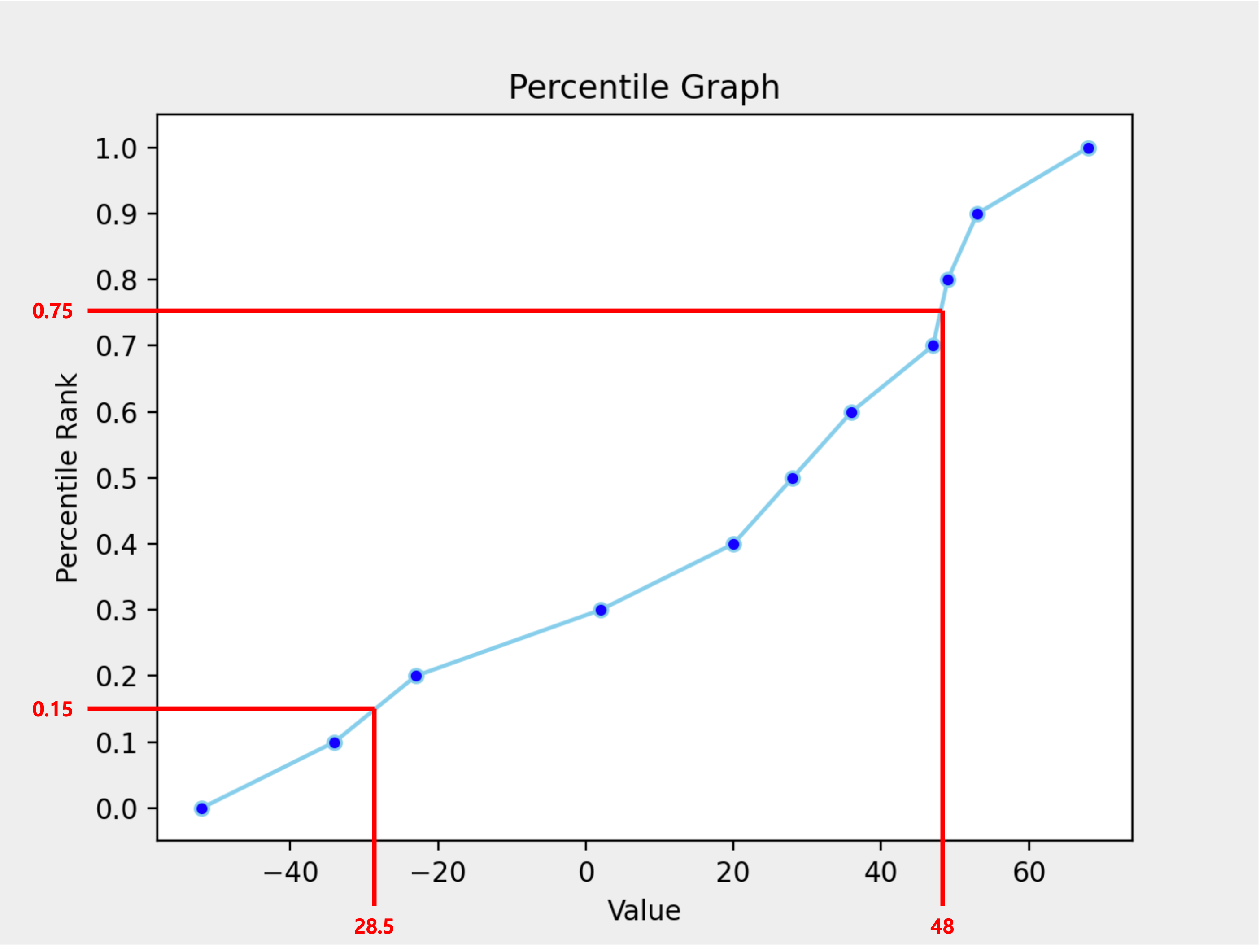
백분위 0.15와 0.75에 대한 백분위수를 나타낸 그래프 입니다.
위처럼 각 구간별로 기울기가 다르기 때문에 반드시 기존 Value들을 기준으로 계산된 가장 인접 구간에서 특정 백분위에 대한 백분위수를 구해야 합니다.
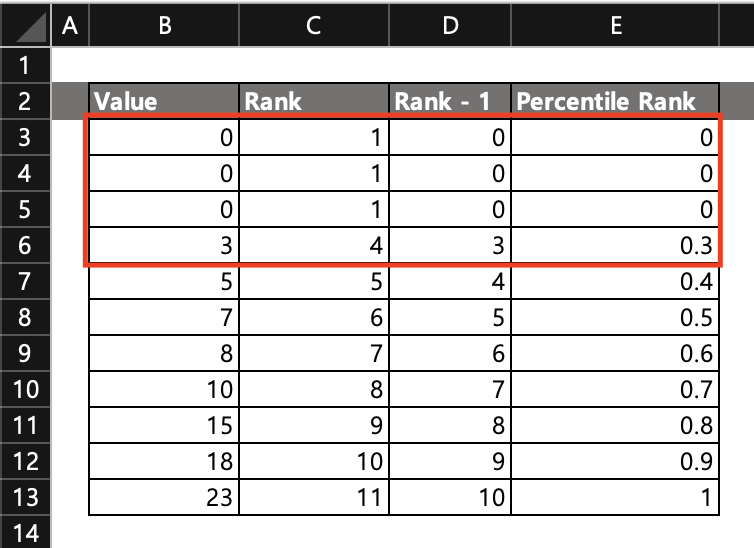
위 예시를 봅시다.
위 예시는 가장 작은 3개의 값이 0으로 동일하며 그 다음 값은 3입니다.
Value = 0은 가장 작은 값이므로 값 0의 백분위는 모두 0입니다.
그리고 Value = 3의 백분위는 0.3입니다.
그러면 0~0.3 구간의 백분위수를 구해봅시다.

주의깊게 봐야할 구간은 0~0.2 구간입니다.
0~0.2의 백분위수는 모두 0입니다.
백분위수를 구할 땐 반드시 가장 인접한 2개의 Value 사이에서 구해야한다고 했죠.
가장 첫 3개의 값이 모두 0으로 동일했고, 그 다음 Value = 3의 백분위가 0.3이므로 0~0.2까지는 모두 백분위수가 0이 됩니다.
그 이유는 총 11개의 Value가 존재하고 그 중 첫 3개의 값에 대해 이 값들이 0으로 동일하지 않았다면 각각 0, 0.1, 0.2의 백분위를 가졌을 겁니다.
따라서 3번째 값까지 모두 0으로 동일하므로 0.2까지는 모두 가장 인접한 2개의 값 사이에서 백분위를 구하므로 백분위 0.2까지는 백분위수가 모두 0이 됩니다.
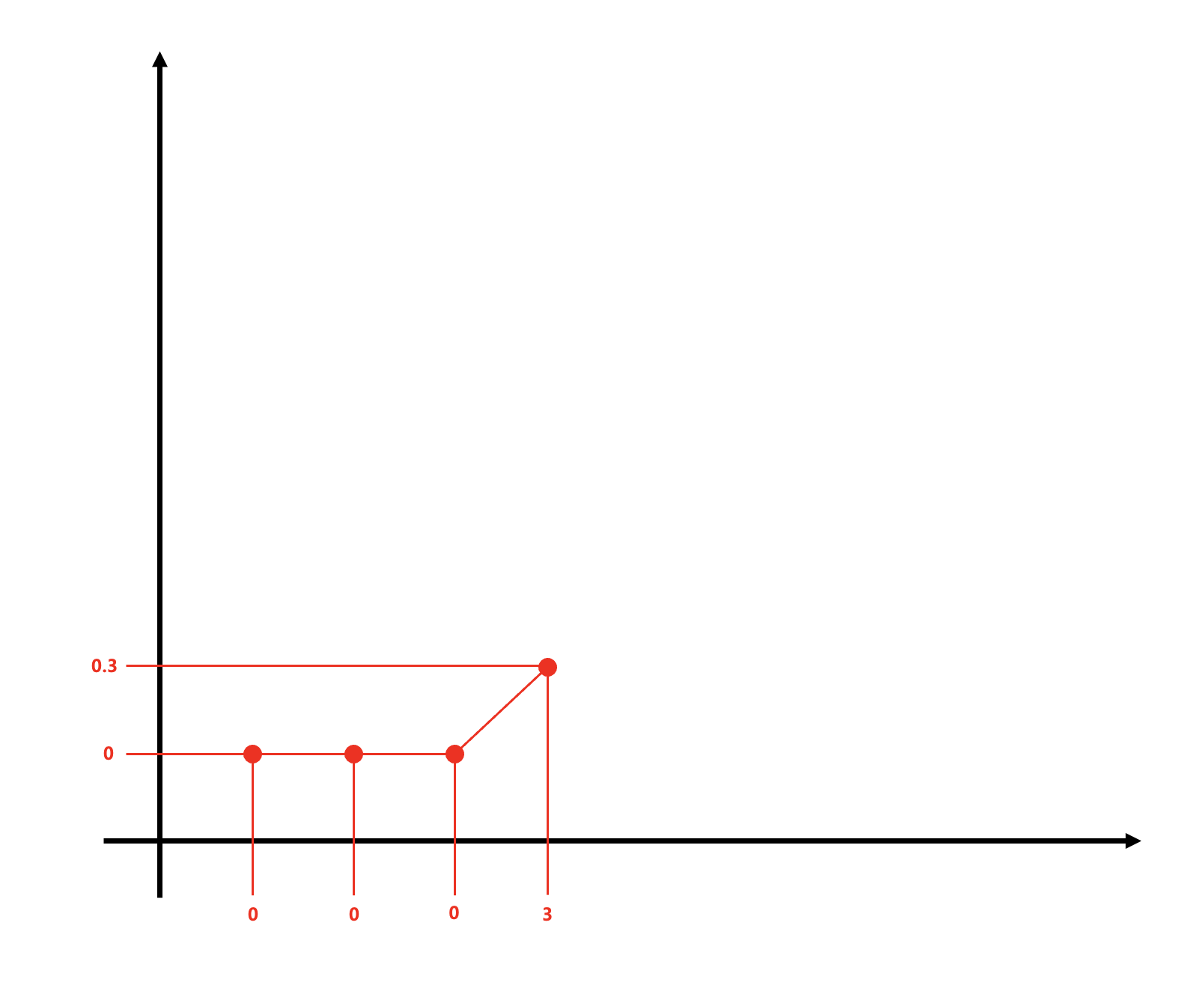
이걸 그래프로 나타내기엔 좀 오류가 있지만
위처럼 세 번째 값까지 값은 0으로 동일하고 백분위수 또한 0으로 동일하기에 여기까진 모두 백분위수 0이 나오게 되죠.
그러다가 0.2를 넘어서면 Value = 0 ~ Value = 3 사이의 구간에 위치하므로 백분위수가 0보다 커지게 됩니다.
4. 사분위수(Quartile)
백분위를 하다보면 사분위수(Quartile)라는 개념이 나옵니다.
보통
n사분위수 (Quartile n)이라고 쓰이는데
1사분위수 (Quartile 1)
2사분위수 (Quartile 2)
3사분위수 (Quartile 3)
4사분위수 (Quartile 4)
이렇게 주로 4개의 값이 존재합니다.
(상황에 따라 0사분위수 라는 값도 언급하곤 합니다.)
이는 특이한 것은 아니고 각각 백분위 25%, 50%, 75%, 100%에 위치하는 값을 의미합니다.
(0사분위수는 백분위 0%에 위치하는 값이구요.)
0사분위수 (Quartile 0) = 백분위 0% 위치에 존재하는 백분위수
1사분위수 (Quartile 1) = 백분위 25% 위치에 존재하는 백분위수
2사분위수 (Quartile 2) = 백분위 50% 위치에 존재하는 백분위수
3사분위수 (Quartile 3) = 백분위 75% 위치에 존재하는 백분위수
4사분위수 (Quartile 4) = 백분위 100% 위치에 존재하는 백분위수
Quartile 2는 백분위 50% 위치에 존재하는 숫자이기 때문에 Quartile 2는 중간값(median)을 의미합니다.
또한 간혹 보면 Quantile이라는 말도 나옵니다.
이는 Quartile과 동일한데 백분위를 어떻게 표현하는지에 따라 다릅니다.
0사분위수 = Quartile 0 = Quantile 0 = Percentile 0
1사분위수 = Quartile 1 = Quantile 0.25 = Percentile 0.25
2사분위수 = Quartile 2 = Quantile 0.5 = Percentile 0.5 -> median
3사분위수 = Quartile 3 = Quantile 0.75 = Percentile 0.75
4사분위수 = Quartile 4 = Quantile 1 = Percentile 1
5. 백분위, 백분위수는 왜/어떻게 쓰이는가?
백분위, 백분위수는 사용하기 나름이라 상당히 다양한 곳에서 사용할 수 있습니다.
특정 시험에서 시험 점수들에 대한 위치를 나타낼 때 가장 많이 들어보셨을겁니다.
다른 사례로는 어떠한 값들이 있을 때 이 값들 중에는 지나치게 비 이상적인 값(Outlier)이 포함되어 있을 수 있습니다.
이럴 때 1사분위수, 3사분위수를 기준으로 하여
(Value <= 1사분위수 - k) or (3사분위수 + k >= Value) 범위에 있는 값을 Outlier로 정의하여 통계치에서 제외하는 방식으로 사용될 수 있습니다.
다양한 예시를 보면 백분위, 백분위수가 사용되는 상황의 공통점은
어떠한 값들이 있고 이 값들의 상대적인 위치가 필요할 때 주로 사용됩니다.
'ETC' 카테고리의 다른 글
| 폰트, Font, TTF, OTF (0) | 2024.03.07 |
|---|---|
| 분산, 표준편차 (0) | 2024.02.20 |
| 2진수의 음수표현 (부호 절대값, 1의 보수, 2의 보수) (4) | 2022.04.07 |
| Window : Window IP 주소 확인 (IP, 윈도우 IP 주소, IP Address) (0) | 2022.02.23 |
| Chrome 기본 언어 설정 (0) | 2022.02.10 |


